[Fe15]: a frustrated, centred tetrakis hexahedron†
The combination of two different FeIII salts in a solvothermal reaction with triethanolamine results in the formation of a high symmetry [FeIII15] cluster whose structure conforms to a centred, tetrakis hexahedron.
The [Fe15O30] core displays a breadth of different Fe–O–Fe angles, ranging from a minimum of 86.67° (Fe4–O5–Fe3) to a maximum of 140.82° (Fe4–O5–Fe2). Angles from the central Fe4 ion to the peripheral Fe1 and Fe2 ions via the O5 oxide are 140.82° and 117.41°, while those connecting the outer Fe1, Fe2 and Fe3 ions together via the oxides and alkoxides range between 86.7–129.39° (Table S2, ESI†). The closest intermolecular interactions are between the monodentate Cl ions on Fe2 and the C-atoms of the tea3− ligands on neighbouring molecules (Cl1⋯C7, ∼3.43 Å), and between the perchlorate O-atoms and the C-atoms of the tea3− ligands (O6⋯C4, ∼3.43 Å; Fig. S6 and S7, ESI†). This results in an aesthetically pleasing honeycomb-like network when viewed down the c-axis of the cell. A search of the CSD reveals that just three [Fe15] clusters have been reported previously,11 with 1 being the first example of a [centred] tetrakis hexahedron. Perhaps more surprisingly, given the widespread use of the H3tea ligand in 3d coordination chemistry, there are very few homometallic FeIII clusters of this ligand deposited. Indeed, they are limited to [Fe5],12 [Fe6] wheels (both unsupported13 and supported14), [Fe7],15 [Fe8]16 (including an [Fe8] cluster self-assembled into a [Fe64] cage17), and [Fe10].18 Heterometallic Fe–Ln species are far more prevalent.19
The direct-current (dc) molar magnetic susceptibility, χ, of a polycrystalline sample of 1 was measured in an applied magnetic field, B, of 0.1 T, over the 2–300 K temperature, T, range. The results are plotted in Fig. 3 in the form of χT product, where χ = M/B with M the magnetisation. At room temperature, the χT product is 28.67 emu K mol−1, much lower than the Curie constant expected for fifteen uncorrelated S = 5/2 centres (65.625 emu K mol−1) with g = 2. On lowering the temperature, the χT product decreases rapidly, reaching a value of 11.05 emu K mol−1) at T = 10 K, before decreasing even more abruptly to a value of 7.74 emu K mol−1 at T = 2 K. The data is therefore indicative of competing antiferromagnetic exchange interactions, and a ground state spin of S ≈ 9/2 (compare arrows in Fig. 3). Variable-temperature-variable-field (VTVB) dc magnetisation measurements in the temperature range 2–6 K and in applied magnetic fields up to 7 T reach a maximum value of just M = 8.35 μB (Fig. 3b), well below the upper limit expected for a ferromagnetically coupled system (M = 75 μB for g = 2). This behaviour is clearly indicative of relatively strong antiferromagnetic interactions between the FeIII ions, consistent with the Fe–O distances and Fe–O–Fe angles present.1
It is computationally impossible to quantitatively analyse the magnetic data of a molecule containing 15 × S = 5/2 spins via conventional matrix diagonalisation techniques since the dimension of the Hilbert space is 470,184,984,576 and thus we turn to the finite-temperature Lanczos method.20 Even here, several assumptions must be made. (A) Despite the presence of eight independent exchange interactions, we reduce this to four based on similar Fe–O bond lengths and Fe–O–Fe angles (Fig. S8, ESI†). These are: Jcube along edges of the cube; Jpyramid along the four edges from the top of each pyramid to the respective base square of the cube; Jc,cube from the central Fe inside the cube to vertices of the cube; and Jc,pyramid from the central Fe ion to the tops of pyramids. (B) We simulate the data using isotropic S = 3/2 spins rather than isotropic S = 5/2 spins and scale the resulting data accordingly. The corresponding isotropic spin-Hamiltonian is:
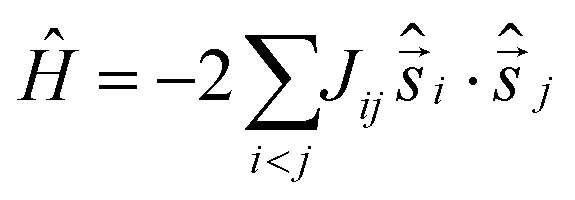
where Jij denotes the four employed exchange constants, respectively. A rather good theoretical representation of the data (Fig. 3) was obtained with Jcube = −17.4 cm−1, Jpyramid = −17.4 cm−1, Jc,cube = −17.4 cm−1 and Jc,pyramid = −3.5 cm−1, scaled by 9/25 to meet a Hamiltonian with spins S = 5/2. Such a scaling approach can only provide “an order of magnitude” estimate of the exchange constants, rather than a precise derivation, albeit the numbers are entirely consistent with experimentally and computationally derived magneto-structural correlations for O-bridged FeIII clusters.21 The exchange constants are indicative of a highly frustrated system, as one might expect from the structural symmetry. Heat capacity, C, measurements were collected between ∼0.3 K and 30 K, for B = 0, 3 and 7 T (Fig. S9, ESI†). Below ∼3 K, the heat capacity depends significantly on B, the zero-field C showing essentially flat behaviour and reaching values close to ∼0.5R, where R is the gas constant. This behaviour is similar to that recently reported for an [Fe III10Gd III10] wheel22 and consistent with the presence of a large density of low-lying states, likely resulting from competing antiferromagnetic interactions.
To further support the relative sign and magnitude of the coupling constants obtained, we have performed DFT calculations (see the ESI† for the Computational details) on a model complex, 1A, derived from complex 1 (Fig. S10 and S11, ESI†). These suggest that the eight independent exchange interactions are in the range |J| = 4.6–16.4 cm−1 (Table S3, ESI†), in good agreement with the experimental simulations. All are antiferromagnetic in nature, with the exception of the Fe4–(μ4-O2−)3–Fe3 interaction which affords J = +4.6 cm−1 on account of the large Fe–O bond lengths and small Fe–O–Fe bond angles present which lead to orbital orthogonality. Overlap integral calculations23 using metal-based singly occupied molecular orbitals (SOMOs) reveal that the strongest antiferromagnetic interactions occur where there are a higher number of strong or moderate overlap integrals, and vice versa (Fig. S12 and S13, ESI†). For the Fe4–(μ4-O2−)3–Fe3 interaction (J1 in Tables S3 and S4, ESI†) there is only one strong interaction (dz2||dxz) with the remaining 24 interactions being weak. The overall result is a weak/moderate ferromagnetic interaction. See the ESI† for more information. Spin density analysis suggests that strong spin delocalisation is present in 1 with FeIII spin densities ranging between 4.007–4.151 (Fig. S14, ESI†).
It is somewhat unusual for synthetic chemists to employ two different metal salts for the formation of homometallic cluster compounds containing paramagnetic 3d metals, since the anions are often considered solely as charge balancing moieties rather than structure-directing agents. This observation has certainly prompted us to re-examine a number of reactions to probe whether it may be of general applicability, or if it is of more limited scope. Here, the use of both FeCl3, Fe(ClO4)3·6H2O with teaH3 in a high temperature, high pressure reaction leads to the formation of an aesthetically pleasing [Fe15] cage conforming to a centred, tetrakis hexahedron. The high symmetry of the metallic skeleton leads to the presence of competing antiferromagnetic exchange interactions and spin frustration. Use of the finite temperature Lanczos method allows for “an order of magnitude” estimation of the exchange constants present, a computationally non-trivial task for a molecule containing fifteen S = 5/2 spins. Values of Jcube = −17.4 cm−1, Jpyramid = −17.4 cm−1, Jc,cube = −17.4 cm−1 and Jc,pyramid = −3.5 cm−1 are consistent with parameters obtained from DFT calculations which fall in the range +4.6 to −16.4 cm−1, and with low temperature heat capacity data which reflects the presence of a large density of low-lying spin states.
EKB and LC thank U21/EPSRC for funding a studentship (DJC). MKS would like to thank Edinburgh Compute and Data Facility (ECDF), and the European Union Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 832488. ME thanks the Spanish Ministry of Science and Innovation (Project RTI2018-098537-B-C22).